[ad_1]
Qu’est-ce que fuzzy matching?
Fuzzy matching (également appelée correspondance approximative de chaînes) est une technique qui permet d’identifier deux éléments de texte, chaînes ou entrées qui sont à peu près similaires mais ne sont pas exactement identiques.
Par exemple, prenons le cas d’une liste d’hôtels à New York comme le montrent Expedia et Priceline dans le graphique ci-dessous.
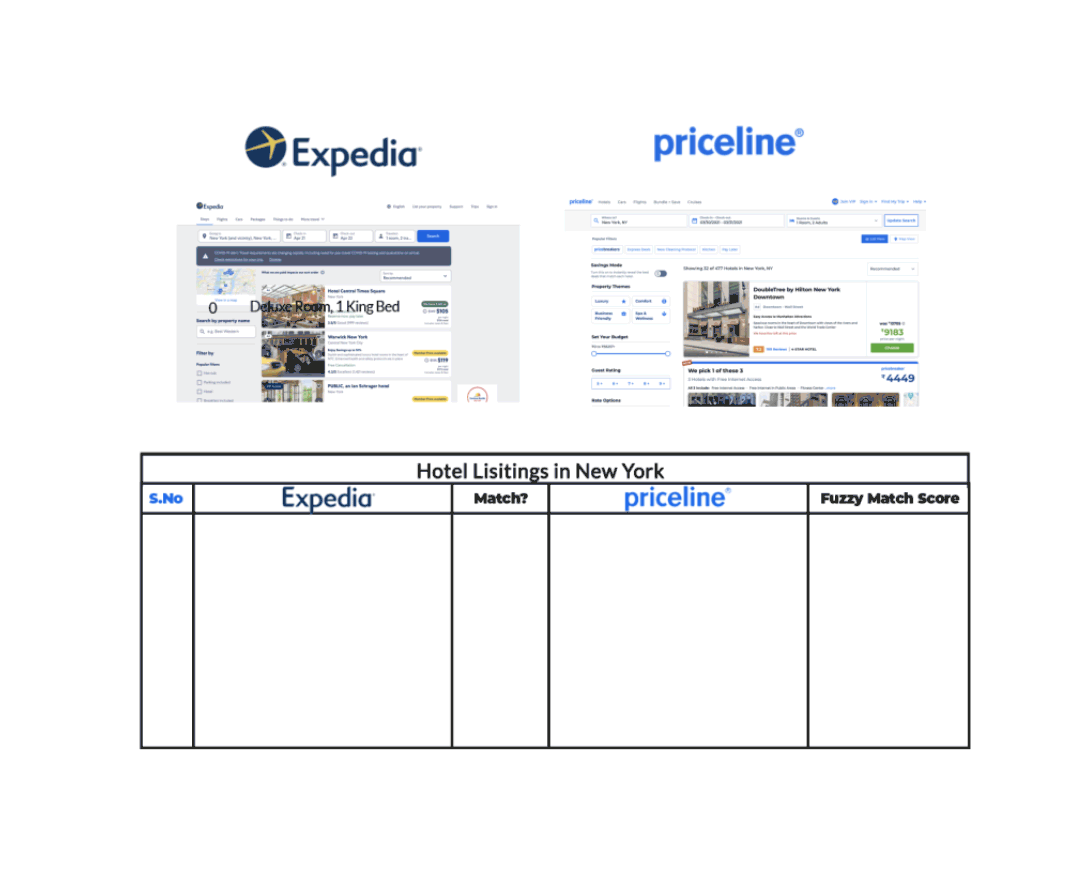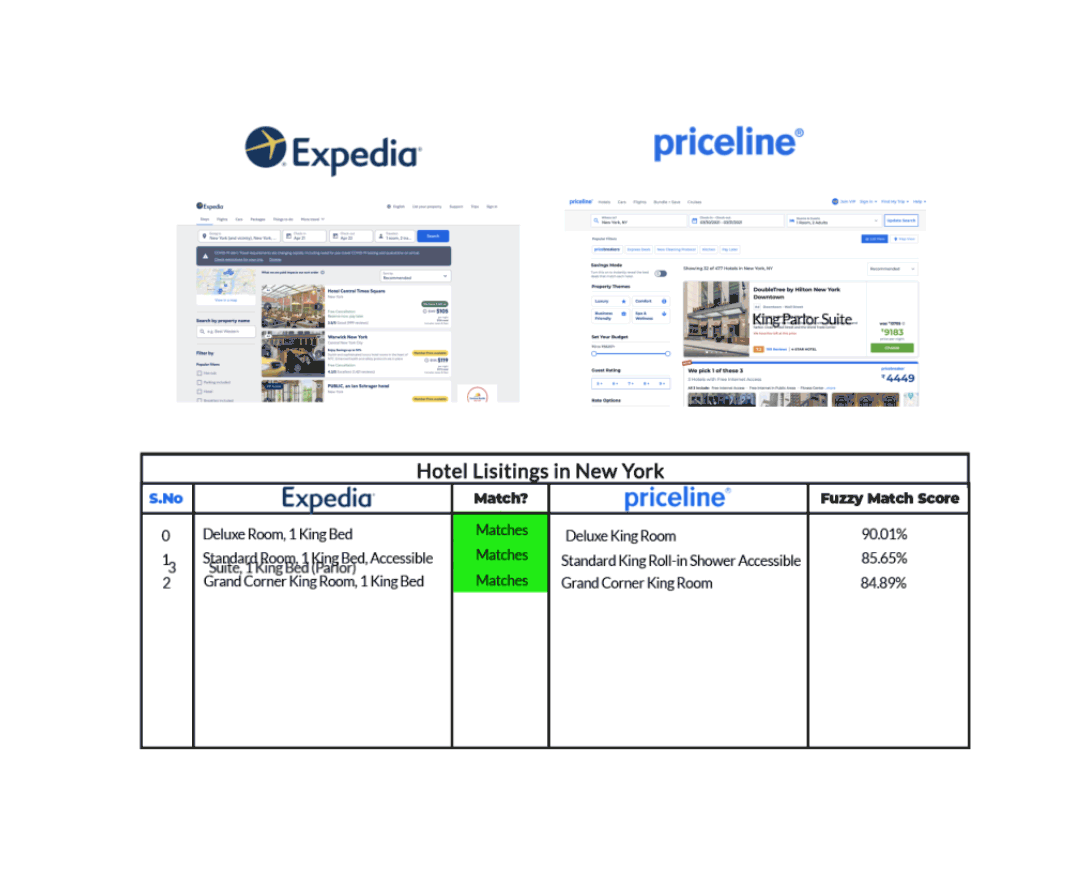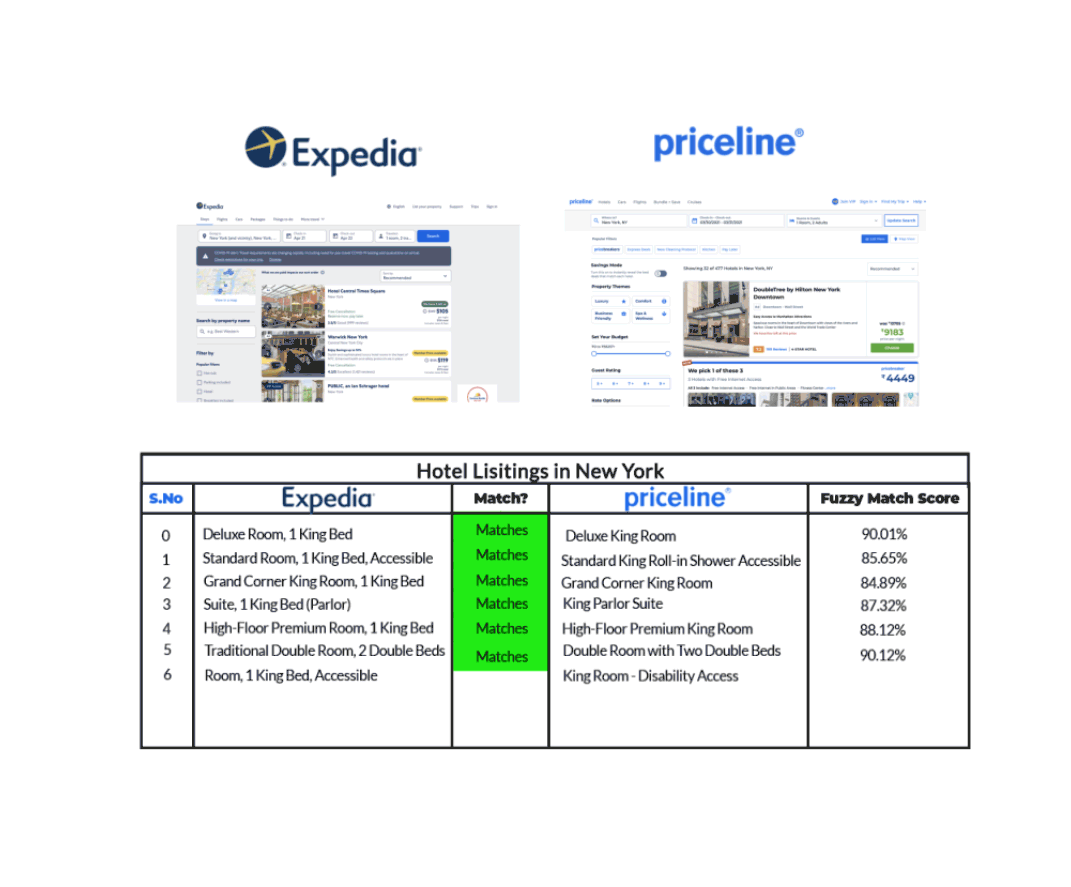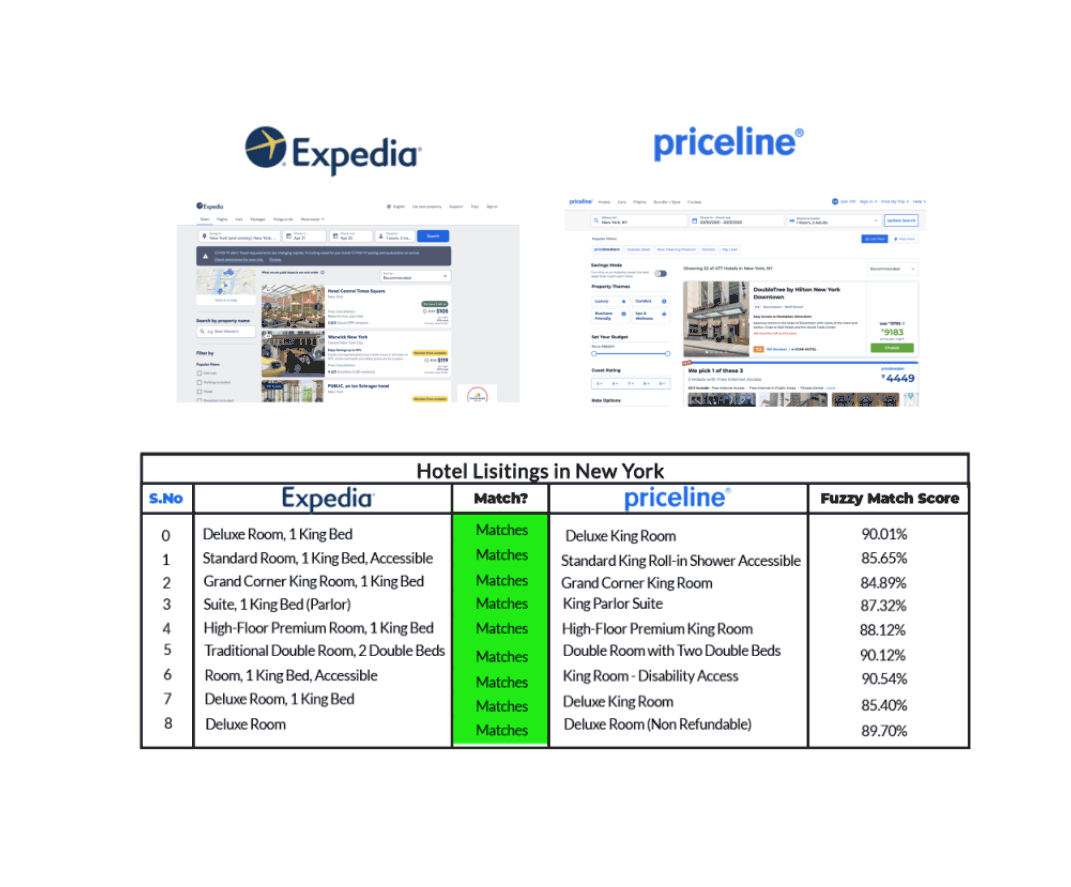
Nous pouvons voir qu’Expedia et Priceline décrivent la même annonce de manières légèrement différentes. Grâce à la fuzzy matching qui identifie deux morceaux de texte à peu près similaires, nous sommes en mesure de faire correspondre la même liste d’hôtels sur chacun de ces sites, même si leurs descriptions ne sont pas exactement les mêmes.
Il existe de nombreuses situations dans lesquelles les techniques de fuzzy matching peuvent s’avérer utiles. Examinons quelques exemples concrets d’utilisation de Fuzzy Matching.
1) Création d’une vue client unique (SCV) : une vue client unique (SCV) fait référence à la collecte de toutes les données sur les clients et à leur fusion en un seul enregistrement.
Par exemple : supposons que vous gérez un restaurant. Vous pouvez disposer des sources de données/tables suivantes. Le tableau 1 contient des informations sur l’historique des commandes de vos clients et le tableau 2 contient des informations sur leurs habitudes de navigation sur le site Web du restaurant.
Une grande organisation dispose forcément d’une multitude de tables de ce type qu’elle peut rejoindre pour obtenir une vue client unique. Cela nécessite souvent une correspondance de chaîne floue (dans notre scénario, les tableaux 1 et 2 doivent être joints à l’aide de l’attribut Nom du client).
Le restaurant pourrait exploiter les informations SCV comme suit :
lorsqu’un client régulier appelle pour passer une commande, le restaurant pourrait suggérer un nouveau plat en fonction de son historique de commandes et des recettes qu’il a consultées. Le restaurant pourrait également envoyer du contenu personnalisé (nouvelles recettes passionnantes) à ses clients en utilisant les informations SCV.
2) Exactitude des données :
Selon une étude récente, plus de 60 % des entreprises ont mis en œuvre des solutions basées sur le Machine Learning. Alors que les entreprises s’appuient sur l’intelligence artificielle et l’apprentissage automatique, l’exactitude des données devient extrêmement cruciale.
Des recherches révolutionnaires sont souvent menées pour améliorer la précision des réseaux neuronaux et des technologies d’apprentissage automatique, mais peu d’efforts sont faits pour garantir que des données de bonne qualité soient transmises à ces modèles. Un excellent algorithme d’apprentissage automatique sans données précises équivaut au lancement d’une fusée sur Mars à l’aide de gaz naturel comprimé.
La correspondance de chaînes floues peut contribuer à améliorer la qualité et la précision des données grâce à la déduplication des données, à l’identification des faux positifs, etc.
3) Détection de fraude :
Un bon algorithme de correspondance de chaînes floues peut aider à détecter la fraude au sein d’une organisation. Plus loin dans cet article, nous verrons comment la FAA a utilisé la correspondance de chaînes floues pour identifier plusieurs pilotes ayant présenté un comportement frauduleux.
Cas d’utilisation intéressants de fuzzy matching
1) Correcteur orthographique (Source : http://norvig.com/spell-correct.html )
De nos jours, la plupart d’entre nous ne prennent même pas la peine de trouver l’orthographe correcte lors de la rédaction d’un e-mail, telle est la confiance que nous accordons aux correcteurs orthographiques modernes.
Dans les paragraphes suivants, je tenterai de décrire les principes de base d’un simple correcteur orthographique.
L’équation suivante est utilisée pour trouver la correction la plus probable :
Ici, P(c) indique la fréquence à laquelle le mot « c » est utilisé dans la langue anglaise. Il peut être calculé en comptant le nombre de fois qu’un mot apparaît dans un grand corpus de texte. P(w|c) est la probabilité que l’auteur ait tapé le mauvais mot « w » au lieu du bon mot « c ». P(w|c) dépend de notre modèle d’erreur.
Les étapes suivantes permettent de connaître une orthographe corrigée :
i) L’étape floue : trouver tous les mots valides possibles ayant des distances d’édition (nombre minimum de substitutions, d’insertions ou de suppressions de caractères uniques requises pour transformer une chaîne en l’autre) de 1 et 2 par rapport au mot donné.
(ii) Le modèle d’erreur : supposons que les mots à une distance d’édition de 1 sont plus probables que les mots à une distance d’édition de 2 (normalement, quelque chose de plus sophistiqué devrait être utilisé pour le modèle d’erreur).
Puisque nous avons P(c) et P(w|c), nous pouvons trouver la correction la plus probable. En parcourant l’algorithme, nous pouvons voir qu’il combine simplement la correspondance de chaînes floues avec la théorie des probabilités pour construire un correcteur orthographique simple mais efficace.
2. Classification des données génomiques (Source : http://www.ipcsit.com/vol30/019-ICNCS2012-G1021.pdf )
Dans ce travail, les auteurs étudient le problème consistant à tenter de déterminer le groupe d’une séquence génomique invisible. Les auteurs résolvent le problème de l’identification des groupes en utilisant une vaste base de données de séquences génomiques.
Ils essaient de faire correspondre la séquence de requête (la séquence inconnue) avec des candidats potentiels dans la base de données.
La correspondance exacte n’est pas très utile, car la séquence de requête correspond rarement exactement aux séquences du génome de la base de données. Pour résoudre ce problème, les auteurs effectuent une fuzzy matching entre la séquence de requête et la base de données génomique.
Les correspondances sont ensuite transmises en tant qu’entrées à un classificateur (SVM, rétropropagation, etc.) qui détermine le groupe du génome.
J’espère que vous êtes convaincu que la fuzzy matching des noms est un sujet important et qu’il vaut la peine d’y consacrer du temps.
La logique traditionnelle est de nature binaire, c’est-à-dire qu’une affirmation est vraie ou fausse. Dans l’exemple précédent, un enregistrement de la Table1 correspondait exactement à un enregistrement de la Table2 ou non.
Au contraire, la logique floue indique dans quelle mesure une affirmation est vraie. Par exemple, des règles floues peuvent indiquer que les annonces sous Expedia correspondent potentiellement à la même annonce sous Priceline.
Comprendre la fuzzy matching avec un exemple du monde réel
Essayons de comprendre le concept de fuzzy matching en considérant un exemple concret. La figure 4 montre le schéma de base de données d’une petite organisation.
Si on vous confiait la tâche de joindre plusieurs tables au sein de ce schéma pour créer une vue unique pour les données client ou produit, comment procéderiez-vous ?
En théorie, si toutes les données étaient parfaitement propres (pas de doublons, pas de mots mal orthographiés, etc.), nous pourrions effectuer l’opération de jointure en utilisant les clés primaires et secondaires appropriées. Cependant, les données du monde réel sont souvent très imparfaites, désordonnées et inexactes.
Une enquête menée par Gartner souligne que « la mauvaise qualité des données est l’une des principales raisons pour lesquelles 40 % de toutes les initiatives commerciales ne parviennent pas à atteindre les avantages escomptés » ( https://www.data.com/export/sites/data/common/assets ). /pdf/DS_Gartner.pdf ).
Étant donné que les données du monde réel sont forcément compliquées, comment procéderions-nous pour joindre des tables individuelles ? Prenons l’exemple illustré à la figure 5.
Supposons que nous souhaitions joindre les tables « Clients » et « Commandes » en fonction de l’attribut customer_name. Nous pourrions utiliser une règle déterministe basée sur des correspondances strictes entre les enregistrements de la table1 et de la table2.
Par exemple, un nom de client « John Chambers » dans le tableau 1 correspond à toutes les occurrences du même nom de client (« John Chambers ») dans le tableau 2.
Bien que cette approche soit théoriquement valable, elle fonctionne rarement en pratique. Par exemple, si le nom « John Chambers » est mal orthographié comme « Jon Chamber » dans le tableau 2, la jointure résultante serait incohérente. Comment pourrions-nous résoudre un tel problème ?
La fuzzy matching peut être utile dans de tels scénarios.
L’un des cas d’utilisation les plus importants de la fuzzy matching survient lorsque nous souhaitons joindre des tables à l’aide du champ de nom.
Pour comprendre le problème de la fuzzy matching floue des noms, considérons le problème suivant.
Disons qu’une société de marketing envoie un questionnaire à de nombreuses personnes. Certaines personnes prennent le temps de remplir le questionnaire tandis que d’autres ne s’en donnent pas la peine. Désormais, la même entreprise envoie un questionnaire différent après 6 mois au même groupe de personnes.
L’entreprise stocke les réponses aux premier et deuxième questionnaires dans deux tableaux distincts. Pour fusionner les informations collectées, l’entreprise souhaiterait joindre les tables 1 et 2 en utilisant l’attribut « nom » comme clé primaire.
Cependant, rien ne garantit qu’une personne remplira exactement le même nom dans le premier et le deuxième questionnaire. Par exemple, une personne dont le nom officiel est « Dr. Jack Murphy » pourrait remplir « Jack » dans le premier questionnaire et « Dr Jack » dans le deuxième questionnaire. Les faire correspondre nécessite un ensemble de règles capables de gérer de légères variations dans le champ de nom. Ces ensembles de règles sont appelés règles floues et nous appelons ce processus Fuzzy Name Matching.
Formalisons le problème. Nous avons une base de données avec ‘n’ tables que nous souhaitons rejoindre en utilisant l’attribut name. Utiliser une règle stricte selon laquelle nous imposons que chaque caractère d’un nom dans la table1 doit correspondre exactement à chaque caractère d’un nom dans la table2 n’est pas pratique, comme le montre clairement l’exemple ci-dessus.
Par exemple, l’ensemble de règles que nous formulons devrait pouvoir faire correspondre le nom « Mike Daniel » dans le tableau 1 avec « Mike D », « Dr. » Mike’, ‘MikeDaniel’ etc.
La correspondance de noms floue est-elle vraiment utile ? Une étude de cas sur l’utilisation de la correspondance de noms floue pour détecter la fraude
(Source : https://dataladder.com/whitepapers/how-best-in-class-fuzzy-matching-solutions-work-combining-established-and-proprietary-algorithms/ )
Lorsqu’une base de données composée de 40 000 pilotes d’avion a été comparée à une base de données composée de personnes recevant des prestations d’invalidité de la sécurité sociale, les dossiers de quarante pilotes sont apparus dans les deux bases de données.
Cela signifiait que soit les individus mentaient sur leur maladie pour recevoir des prestations d’invalidité, soit ils volaient avec ces maladies, deux infractions punissables.
La logique floue est au cœur de cette opération puisque les noms des pilotes devaient correspondre sur plusieurs tables.
Il existe de nombreux algorithmes populaires qui peuvent être utilisés pour effectuer une correspondance de noms floue. La section suivante parle de certains de ces algorithmes populaires de correspondance de noms flous.
Algorithmes de correspondance de noms flous
1) Distance de Levenshtein :
La distance de Levenshtein est une métrique utilisée pour mesurer la différence entre 2 séquences de cordes.
Il nous donne une mesure du nombre d’insertions, de suppressions ou de substitutions de caractères uniques nécessaires pour transformer une chaîne en une autre.
Mathématiquement, on peut définir la distance de Levenshtein comme suit :
Où tail (a) est une chaîne comprenant tous les caractères de la chaîne a à l’exclusion du premier caractère. D’après la définition, il est clair que la distance de Levenshtein fonctionne bien avec les noms mal orthographiés.
Par exemple, la distance de Levenshtein (le nombre d’insertions, de suppressions ou de substitutions d’un seul caractère) entre les chaînes JOHN (comme on l’écrit aux États-Unis) et JOHAN (comme on l’écrit au Japon, en Suède et en Norvège) ‘ est de 1 comme montré sur la Fig7.
L’inconvénient le plus évident de l’utilisation de la distance de Levenshtein est qu’elle ne prend en compte que la différence dans la manière dont nous épelons les mots.
Par exemple, la distance de Levenshtein entre les mots « ROBERT » et « BOBBY » est de 4. (REMARQUE : Bobby est le surnom de Robert)
2) L’algorithme Soundex :
Soundex est un algorithme phonétique utilisé pour rechercher des noms qui se ressemblent mais sont orthographiés différemment.
Il est le plus souvent utilisé pour les recherches dans les bases de données généalogiques.
L’algorithme Soundex génère un code à 4 chiffres nommé. (La page Wikipédia https://en.wikipedia.org/wiki/Soundex explique bien l’algorithme Soundex)
Par exemple, les noms « Stuart » et « Stewart » produisent le même code Soundex S363.
3) Les algorithmes métaphone et double métaphone :
L’algorithme Metaphone est une amélioration par rapport à l’algorithme vanille Soundex, tandis que l’algorithme double Metaphone s’appuie sur l’algorithme Metaphone.
L’algorithme « double » Metaphone renvoie deux clés pour les mots qui ont plus d’une prononciation.
Considérons l’exemple suivant :
Soundex (« Phillip ») = P410
Soundex (« Fillipe ») = F410
Double métaphone (« Phillip ») = FLP
Double métaphone (« Fillipe ») = FLP
Nous pouvons clairement voir que l’algorithme Doublemetaphone est beaucoup plus robuste que l’algorithme Soundex.
Désavantages:
Un cas d’échec que j’ai rencontré a eu lieu lorsque j’ai utilisé le nom de Jésus (prononcé Haysoos en espagnol).
Double métaphone (‘Jésus’) = (‘JSS’, ‘ASS’)
Double métaphone (‘Haysoos’) = (‘HSS’, ‘ ‘)
4) Similitude cosinus :
Cosinus La similarité entre deux vecteurs non nuls est égale au cosinus de l’angle qui les sépare.
Si nous représentons chaque chaîne (nom) par un vecteur, nous pouvons comparer les chaînes en mesurant l’angle entre leurs représentations vectorielles correspondantes.
Si les vecteurs sont parallèles (theta=0 et cos(theta)=1) alors ils sont égaux les uns aux autres, cependant, s’ils sont orthogonaux (theta=90 degrés et cos(theta)=0), ils sont différents.
Comprenons les différentes étapes impliquées dans le calcul de la similarité cosinus entre deux mots avec un exemple simple. Exemple : Nom1 = « Johan », Nom2 = « Jean ».
i) Divisez les noms dans leurs représentations « n-gram » correspondantes.
ii) Vectorisez chaque n-gramme en utilisant une technique d’encodage. Les techniques de codage les plus couramment utilisées sont le codage par sac de mots ou le codage tf-idf.
iii) Calculez la similarité cosinusoïdale entre les vecteurs.
La figure 8 illustre toutes les étapes impliquées dans le calcul de la similarité cosinusoïdale entre les vecteurs.
Remarque : j’ai été assez surpris lorsque j’ai tapé « Ressources d’apprentissage automatique pour la fuzzy matching ». Pour une fois, je n’ai pas été inondé de centaines d’articles et de leurs référentiels GitHub correspondants.
Les personnes intéressées peuvent se référer au lien suivant : https://www.cs.utexas.edu/~ml/papers/marlin-dissertation-06.pdf et au référentiel GitHub correspondant. Il explique les mesures de similarité apprenables qui peuvent être entraînées pour effectuer un couplage, un regroupement et un blocage précis des enregistrements.
Vous envisagez une fuzzy matching pour votre produit ou votre solution ? Lis ça…
Cette section fournit quelques indications sur la façon dont vous pouvez utiliser la correspondance de chaînes floues pour améliorer le flux de travail existant dans votre produit ou solution.
Supposons que votre équipe commerciale ait du mal à déployer du contenu/des produits personnalisés pour des clients potentiels en raison d’une mauvaise gestion du stockage des données.
Votre meilleur pari est de créer une vue client unifiée qui aiderait votre équipe commerciale à atteindre ses objectifs. Vous décidez d’implémenter un ou plusieurs algorithmes de correspondance de chaînes floues pour faire le travail. Voici quelques points que vous devez garder à l’esprit.
i) Temps et ressources requis :
en général, il est logique d’investir une quantité décente de temps et de ressources dans la configuration du logiciel de correspondance de chaînes floues en fonction de votre cas d’utilisation spécifique.
Des tests unitaires rigoureux sont bénéfiques, surtout si votre cas d’utilisation exige une grande précision. La bonne nouvelle est qu’une fois la configuration du logiciel terminée, la majeure partie du flux de travail peut être automatisée.
En prenant l’exemple de la génération d’une vue client unifiée, le logiciel de fuzzy matching doit simplement être exécuté à intervalles réguliers pour garantir que votre vue client est mise à jour.
ii) Fiabilité : en supposant que vous ayez consacré le temps nécessaire à la configuration du logiciel, quelle serait sa fiabilité ? Presque tous les algorithmes de correspondance de chaînes floues sont voués à générer des faux positifs.
Cela signifie généralement une vérification manuelle des erreurs. Vous devez trouver le bon équilibre entre le nombre de faux positifs, la quantité de main d’œuvre que vous pouvez vous permettre pour vérifier les erreurs et l’effet que les faux positifs auraient sur votre entreprise.
Par exemple, si des faux positifs amènent un client à recevoir une publicité pour une recette de pâtes au lieu d’une recette de pizza, vous êtes du bon côté.
Quelques bonnes pratiques et faits à considérer…
a) La correspondance de chaînes floues est un domaine largement étudié et de nouveaux algorithmes/logiciels sont périodiquement publiés. Il vaut la peine de garder les yeux et les oreilles ouverts aux nouveaux développements.
b) Même après des tests rigoureux, vous obtiendrez forcément quelques faux positifs. Assurez-vous de ne pas utiliser de logiciel flou pour traiter des données sensibles.
c) La correspondance de chaînes floues rapporte les dividendes les plus élevés lorsque vous disposez d’un grand nombre de données qui, si elles sont correctement mises en correspondance, entraînent un avantage important, tandis que les faux positifs n’ont pas beaucoup d’importance.
Implémentation de la fuzzy matching dans différents langages de programmation
Voyons comment les algorithmes de Fuzzy Matching peuvent être implémentés dans différents langages de programmation.
Nous implémenterons la correspondance de chaînes floues dans divers langages de programmation sur l’ensemble de données du restaurant.
L’ensemble de données contient 864 enregistrements de restaurants provenant des guides de restaurants Fodor’s et Zagat qui contiennent 112 doublons. (Source : https://www.cs.utexas.edu/users/ml/riddle/data.html ).
Nous illustrons une application importante de la correspondance de chaînes floues, à savoir la détection des doublons . Par exemple : considérez la figure 10.
On voit bien que le premier et le deuxième enregistrement correspondent au même restaurant, de même, le troisième et le quatrième enregistrement correspondent au même restaurant. Notre objectif est de découvrir tous les doublons dans la base de données en utilisant la correspondance de chaînes floues.
Dans le processus d’implémentation de la détection des doublons à l’aide de divers langages de programmation, nous passons en revue certains des packages intégrés fournis par ces langages de programmation, à l’aide desquels presque toute la complexité est abstraite du programmeur.
Pour simplifier le problème, nous tenterons de détecter les doublons uniquement en utilisant le champ nom.
Correspondance de chaînes floues à l’aide de Python
Présentation de Fuzzywuzzy : Fuzzywuzzy est une bibliothèque Python utilisée pour la correspondance de chaînes floues. La métrique de comparaison de base utilisée par la bibliothèque Fuzzywuzzy est la distance de Levenshtein.
En utilisant cette métrique de base, Fuzzywuzzy fournit diverses API qui peuvent être directement utilisées pour la fuzzy matching. Passons en revue tout le pipeline de détection des doublons.
i) Prétraitement des données :
Puisque nous détectons les doublons en utilisant uniquement le champ « nom », lors de l’étape de prétraitement (nettoyage des données), nous convertissons le nom entier en minuscules et supprimons la ponctuation des noms. L’extrait de code de la figure 11 illustre ce processus.
ii) Création d’un index :
Une manière naïve de faire correspondre les enregistrements dans une table consiste à comparer chaque enregistrement avec tous les autres enregistrements. Cependant, en utilisant cette méthode, le nombre de paires augmente quadratiquement, ce qui pourrait ralentir l’algorithme.
Nous utilisons le Python Record Linkage Toolkit à l’aide duquel plusieurs méthodes d’indexation telles que le blocage et l’indexation de quartier triée peuvent être implémentées. (REMARQUE : pour notre ensemble de données, nous avons calculé un index complet car il ne contient que 863 enregistrements)
L’extrait de code de la figure 12 illustre la création d’un index pour la comparaison des enregistrements.
iii) Identifier les doublons à l’aide de Fuzzywuzzy :
Les doublons ont été identifiés à l’aide de la méthode partial_ratio de Fuzzywuzzy. Étant donné deux chaînes str1(longueur n1) et str2(longueur n2) telles que n1 > n2, il calcule la distance de Levenshtein entre str2 et toutes les sous-chaînes de longueur n2 dans str1.
Grâce à cette méthode, nous avons identifié 201 doublons.
Correspondance de chaînes floues à l’aide de R
Tout d’abord, je dois avouer que je suis vierge R. Cependant, il s’avère que la programmation en R est extrêmement simple et intuitive. J’ai effectué les mêmes étapes, à savoir le prétraitement des données (conversion des noms en minuscules et suppression de la ponctuation) suivi d’une correspondance de noms floue à l’aide de la métrique de distance de Levenshtein.
L’extrait de code suivant illustre le pipeline utilisé pour la détection des doublons.
La ponctuation a été éliminée en utilisant la fonction gsub . Suite à cela, une matrice a été construite en utilisant la métrique de distance standard de Levenshtein entre les champs de nom.
Enfin, le nombre de doublons a été compté (si la distance de Levenshtein entre deux enregistrements est inférieure à 2, ils sont considérés comme des doublons).
L’algorithme détecte 164 enregistrements en double.
Remarque : L’implémentation ci-dessus n’est pas optimisée.
Correspondance de chaînes floues à l’aide de Java
Les choses étaient un peu plus difficiles en Java car il n’est pas spécifiquement conçu pour la science des données. Cependant, il existe de nombreux référentiels Github disponibles qui effectuent une correspondance de chaînes floues à l’aide de Java.
Le référentiel suivant https://github.com/xdrop/fuzzywuzzy contient une implémentation Java de la bibliothèque Python Fuzzywuzzy. Un exemple simple est présenté sur la figure 14.
REMARQUE : La fonction tokenSortRatio divise les chaînes en jetons, trie les jetons individuels et calcule la distance de Levenshtein entre eux.
Le package de similarité de chaînes Java ( https://github.com/tdebatty/java-string-similarity ) implémente un certain nombre d’algorithmes (distance d’édition de Levenshtein, Jaro-Winkler, LCS, etc.).
Fuzzy matching sans utiliser de code
N’ayez crainte, Microsoft Excel et Stata peuvent vous aider à effectuer une correspondance de chaînes floues à l’aide de l’interface graphique.
Correspondance de chaînes floues à l’aide de Microsoft Excel
Les utilisateurs d’Excel connaissent peut-être la fonction RECHERCHEV utilisée pour rechercher des correspondances exactes entre les colonnes d’un tableau. Excel fournit également un complément de recherche floue utilisé pour effectuer une fuzzy matching entre les colonnes de la version de bureau.
Comme j’utilisais un système d’exploitation basé sur Linux au moment de la rédaction de cet article de blog, je n’ai pas pu utiliser le complément Fuzzy Lookup.
Cependant, la version Web de Microsoft Excel fournit un complément similaire appelé Exis Echo. Il possède une interface extrêmement simple, sélectionnez simplement le nombre souhaité de lignes parmi les colonnes que vous souhaitez faire correspondre et Exis Echo fait le reste.
Comme le montre la figure 17, les restaurants portant les noms « hôtel bel-air » et « hôtel bel-air » sont identifiés comme des doublons (c’est-à-dire qu’ils sont placés dans le même groupe). Cependant, l’algorithme n’identifie pas « l’épicerie fine » et « l’épicerie fine » comme le même restaurant.
Le complément fournit plusieurs paramètres que nous pouvons ajuster pour notre cas d’utilisation spécifique.
Comparaison rapide des logiciels de fuzzy matching
Ce qui suit est une comparaison des différents langages ou logiciels que j’ai utilisés pour implémenter la fuzzy matching.
J’ai attribué une note sur 5, 5 étant la meilleure et 1 la moins bonne.
| Logiciel/Langue utilisé | Facilité d’utilisation | Évolutivité | Vitesse | Note globale totale |
|---|---|---|---|---|
| Python | 4.0 | 4.0 | 3.0 | 11.0 |
| R. | 4.0 | 4.0 | 2.5 | 10.5 |
| Java | 2.0 | 3.0 | 5.0 | 10,0 |
| Microsoft Excel | 5.0 | 1,5 | 3.0 | 9.5 |
Mise à l’échelle de la mise en œuvre de la fuzzy matching
Jusqu’à présent, nous avons envisagé de traiter quelques centaines d’enregistrements à l’aide de la correspondance de chaînes floues. Cependant, dans le monde réel, nous traiterions des milliers, voire des centaines de milliers de documents.
Dans cette section, nous présenterons quelques techniques qui pourraient aider à faire évoluer notre algorithme de correspondance de chaînes floues.
Pour illustrer cela, j’ai utilisé un ensemble de données contenant un grand nombre de noms d’entreprises. Parcourons le code, examinons la fonction de chaque extrait de code et examinons la sortie correspondante.
La cellule ci-dessus charge les données dans une trame de données pandas. Nous pouvons voir que l’ensemble de données contient 1 040 569 entrées.
Certains prétraitements de données sont effectués dans Cell2. Les noms de sociétés sont convertis en minuscules et toute ponctuation en est supprimée.
Nous définissons également une liste de mots vides courants tels que « assn », « inc », etc. que nous supprimons de la liste des noms de sociétés.
Dans Cell3, nous divisons les noms d’entreprise en n-grammes, puis nous vectorisons les noms d’entreprise à l’aide de la fonction Tf-idf. L’étape suivante consiste à calculer la similarité cosinus entre chaque paire de vecteurs dans tf_idf_matrix.
Il est crucial de le faire efficacement pour garantir que l’approche soit bien évolutive.
Scikit-learn fournit une fonction intégrée pour calculer la similarité cosinusoïdale entre les vecteurs. Cependant, l’équipe ING Wholesale Banking Advanced Analytics a créé une bibliothèque personnalisée appelée sparse_dot_topn pour calculer la similarité cosinus à l’aide de Cython (https://github.com/ing-bank/sparse_dot_topn).
Leur mise en œuvre améliore la rapidité d’environ 40 %. J’ai emprunté le code des cellules 4 et 5 sur le site Web suivant : https://bergvca.github.io/2017/10/14/super-fast-string-matching.html .
La matrice « correspondances » contient les indices et les scores de similarité grâce auxquels nous pouvons identifier les doublons. Étant donné que cet ensemble de données n’a pas été spécifiquement conçu pour la détection des doublons ou l’identification des faux positifs, il a déjà été nettoyé et ne contenait aucun doublon.
Remarque : j’ai téléchargé le code sur mon référentiel Github. https://github.com/Varghese-Kuruvilla/Fuzzy_String_Matching .
Je vous encourage à l’utiliser comme référence pour analyser de nouveaux ensembles de données et comprendre les bases de la correspondance de chaînes floues.
Problèmes/problèmes courants rencontrés avec la fuzzy matching et la solution
Dans cette section, je vais essayer de répondre à quelques questions que j’ai vues sur StackOverflow lors de la lecture de cet article de blog. J’encourage les lecteurs à parcourir l’intégralité de l’article pour avoir une bonne compréhension globale de la correspondance de chaînes floues.
1) Comment calculer le score en correspondance de chaînes floues ?
L’un des moyens les plus efficaces de calculer les scores d’un algorithme de correspondance de chaînes floues consiste à utiliser la similarité cosinus. La similarité cosinus entre deux vecteurs non nuls est simplement le cosinus de l’angle entre ces vecteurs.
Ainsi, deux chaînes similaires auraient un score de similarité cosinus plus élevé que deux chaînes différentes. Le succès de cette méthode dépend de la manière dont les chaînes sont converties en leurs représentations vectorielles correspondantes.
Deux des méthodes les plus populaires pour faire de même sont : les extracteurs de fonctionnalités Bag-of-words (BOW) et TF-IDF.
Un extracteur de fonctionnalités BOW calcule la représentation vectorielle d’une chaîne en prenant en compte la fréquence de chaque mot dans le document. Un inconvénient majeur de l’extracteur de fonctionnalités BOW est que des mots comme « le », « de », etc. reçoivent un score très élevé car ils apparaissent très fréquemment dans le document.
TF-IDF tente de surmonter ce problème en utilisant des informations sur le nombre de fois que le mot apparaît dans le document.
Un exemple manuscrit montrant chacune des étapes individuelles du calcul de la similarité cosinus est présenté dans la figure 8.
2) Correspondance de logique floue ( https://stackoverflow.com/questions/37978098/fuzzy-logic-matching )
Pour votre cas d’utilisation de listes de correspondance de noms d’entreprises, je vous suggère de passer en revue les points suivants.
a) Attribut unique : tout d’abord, assurez-vous que vous ne pouvez pas faire de correspondance en utilisant un autre attribut unique comme une adresse, etc. Un attribut unique simplifierait grandement le problème. Après vous être assuré que vous disposez uniquement de l’attribut de nom de société pour la correspondance, vous pouvez procéder aux étapes suivantes.
b) Prétraitement des données : supprimez les mots vides courants du texte. Certains traitements manuels, tels que la sélection des mots qui ne sont pas pertinents pour la liste des noms de sociétés parmi les mots les plus fréquents, s’avéreraient utiles.
c) Indexation : La comparaison de tous les enregistrements est une tâche coûteuse en termes de calcul. Une méthode d’indexation telle que l’indexation par bloc ou par voisinage trié peut être utilisée pour réduire le nombre de comparaisons à effectuer.
d) Fuzzy matching: une mesure telle que la distance de Levenshtein peut être utilisée pour calculer les scores entre des paires de chaînes. Plusieurs implémentations de la distance de Levenshtein sont couvertes dans le package python populaire Fuzzywuzzy.
Pour ce cas d’utilisation, je recommanderais d’utiliser les fonctions token_set_ratio ou partial_ratio.
3) Algorithme de recherche floue ( https://stackoverflow.com/questions/32337135/fuzzy-search-algorithm-approximate-string-matching-algorithm ) :
Le problème peut être décomposé en deux parties :
- Choisir la bonne métrique de chaîne.
- Proposer une mise en œuvre rapide de la même chose.
Choisir la bonne métrique : la première partie dépend largement de votre cas d’utilisation. Cependant, je suggérerais d’utiliser une combinaison d’un score basé sur la distance et d’un codage phonétique pour une plus grande précision, c’est-à-dire en calculant initialement un score basé sur la distance de Levenshtein et plus tard en utilisant Metaphone ou Double Metaphone pour compléter les résultats.
Encore une fois, vous devez baser votre décision sur votre cas d’utilisation, si vous pouvez utiliser uniquement les algorithmes Metaphone ou Double Metaphone, vous n’avez pas à vous soucier beaucoup du coût de calcul.
Implémentation : une façon de limiter le coût de calcul consiste à regrouper vos données en plusieurs petits groupes en fonction de votre algorithme et à les charger dans un dictionnaire.
Par exemple, si vous pouvez supposer que votre utilisateur saisit correctement la première lettre du nom, vous pouvez stocker les noms basés sur cet invariant dans un dictionnaire.
Ainsi, si l’utilisateur saisit le nom « École nationale », vous devez calculer la métrique uniquement pour les noms d’école commençant par la lettre « N ».
Conclusion
J’espère que vous avez passé un bon moment à lire sur la logique floue.
Nous avons d’abord passé en revue le concept de logique floue, leurs applications pratiques et cas d’utilisation, les éléments à prendre en compte si vous choisissez d’utiliser la fuzzy matching, les différents algorithmes utilisés pour implémenter la correspondance de chaînes floues et leur implémentation dans les langages de programmation populaires.
En tant qu’humains, nous sommes souvent incertains de nos décisions, c’est-à-dire que, de par notre nature même, nous sommes flous. Tant que nous restons flous, il est logique que les outils que nous concevons le soient également. Sur cette note plutôt philosophique, je vous retrouverai dans le prochain article du blog.
[ad_2]
Source link